问题
问答题
设F(u，v)有连续的偏导数，a，b，c为常数，Fiu，F’v不同时为零，方程
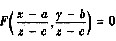确定隐函数z=z(x，y)．
(Ⅰ)求
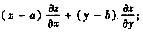
(Ⅱ)证明：曲面z=z(x，y)上任意点(x，y，z)处的切平面通过某定点．
答案
参考答案：[分析与求解] (Ⅰ)方法1° 方程两边分别对x，y求偏导数，注意z=z(x，y)，由复合函数求导法得
[*]
方程两边同乘(z-c)2后分别解出
[*]
因此[*]
方法2° 方程两边求全微分，由微分法则得
[*]
即[*]
化简得[*]
于是[*]
因此，[*]
(Ⅱ)曲面z=z(x，y)上[*]点(x，y，z)处的法向量[*]，于是切平面方程是
[*]
其中(X，Y，Z)是切平面上的动点．按题(Ⅰ)的结论，该切平面经过点(a，b，c)，即
[*]