问题
问答题
设函数f(x)在[0,π]上连续,且
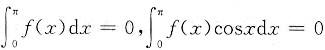 ,试证明:在(0,π)内至少存在两个不同的点ξ1、ξ2,使f(ξ1)=f(ξ2)=0。
,试证明:在(0,π)内至少存在两个不同的点ξ1、ξ2,使f(ξ1)=f(ξ2)=0。
答案
参考答案:本题可采用以下两种方法证明:
[证法1] 引入辅助函数
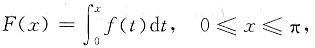
则F(0)=0.F(π)=0.又由
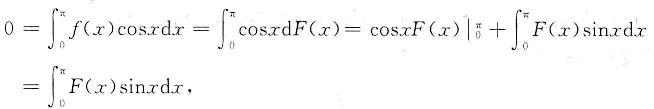
因此必存在一点ξ∈(0,π),使得F(ξ)sinξ=0,否则F(x)sinx在(0,π)内恒正(或负),均与
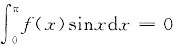 矛盾.
矛盾.
当ξ∈(0,π)时,sinξ≠0,因此F(ξ)=0.综上知
F(0)=F(ξ)=F(π)=0,0<ξ<π.
在区间[0,ξ],[ξ,π]上分别用罗尔定理,则至少存在两点ξ1∈(0,ξ),ξ2∈(ξ,π),使得
F’(ξ1)=F’(ξ2)=0,即 f(ξ1)=f(ξ2)=0.
[证法2] 由已知
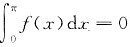 ,知存在ξ1∈(0,π),使f(ξ1)=0.否则f(x)在(0,π)内恒正(或负)。均与
,知存在ξ1∈(0,π),使f(ξ1)=0.否则f(x)在(0,π)内恒正(或负)。均与
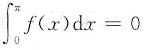 矛盾.若在(0,π)内f(x)仅有一个零点ξ1,则由
矛盾.若在(0,π)内f(x)仅有一个零点ξ1,则由
 可知f(x)在(0,ξ1)与(ξ1,π)内反号.不妨设在(0,ξ1)内f(x)>0,在(ξ1,π)内f(x)<0,因此由
可知f(x)在(0,ξ1)与(ξ1,π)内反号.不妨设在(0,ξ1)内f(x)>0,在(ξ1,π)内f(x)<0,因此由
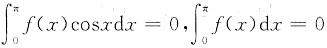 及cosx在[0,π]上的单调性知
及cosx在[0,π]上的单调性知
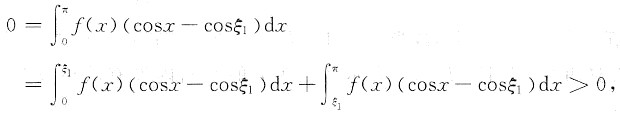
矛盾,由此知在(0,π)内除ξ1外,f(x)至少还有另一个零点ξ2,所以存在ξ1,ξ2∈(0,π)且ξ1≠ξ2,使得f(ξ1)=f(ξ2)=0.
解析:[考点提示] 函数零点、罗尔定理、定积分的性质.
