问题
问答题
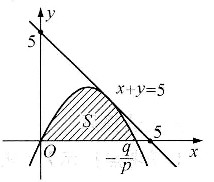
已知抛物线y=px2+qx(其中p＜0，q＞0)在第一象限内与直线x+y=5相切，且此抛物线与x轴所围成的平面图形的面积为S．如右图所示．
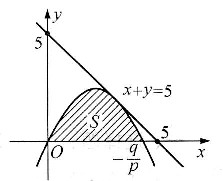
(1) 问p和q为何值时，S达到最大值
(2)求出此最大值．
答案
参考答案：由题设，抛物线与直线的位置关系如右图所示．
抛物线y=px2+qx与x轴的交点为(0，0)及
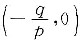，面积S=
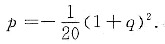
又知抛物线与直线相切，因此两者的公共点唯一，从而方程组
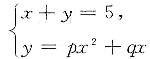有唯一解，可推知
px2+(q+1)x-5=0的根的判别式为0，即△=(q+1)2+20p=0，可解得
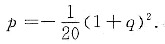
由此，
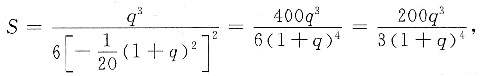
则
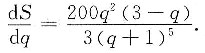
令
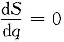，则q=3．
当0＜q＜3时，S’(q)＞0；当q＞3时，S’(q)＜0，所以q=3时，S(q)取极大值，也即最大值，此时，
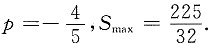
解析：[考点提示] 导数的几何应用、函数最大值．
