如图，一足够长的固定斜面与水平方向成α=37？角，空间有垂直于

问题问答题

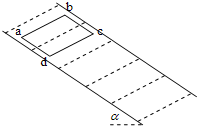
如图，一足够长的固定斜面与水平方向成α=37？角，空间有垂直于斜面的无限多个匀强磁场，其磁感应强度的大小均为B=0.5T，相邻磁场区域的磁场方向相反．每个磁场区域的宽度均为L₁=0.1m，磁场区的边界均与斜面底边平行．现有一质量为m=0.05kg、电阻为R=0.5Ω的矩形金属框abcd沿此斜面下滑，已知ad=L₁=0.1m，ab=L₂=0.2m，下滑过程中，金属框的ab边始终与斜面底边平行，金属框与斜面间的动摩擦因数为μ=0.2，金属框下滑距离s=3m时速度达到最大，求：

（1）金属框下滑的最大速度；

（2）当金属框下滑的加速度为a=2m/s²时，金属框的焦耳热功率；

（3）从开始下滑到速度达到最大的过程中金属框中产生的焦耳热量．

答案

（1）金属框做加速度逐渐减小的加速运动，直到最后运动运动为止，当匀速时速度达到最大，此时有：

mgsinα=F_f+2BIL₂

mgsinα=μmgcosα+

4B2L22vm

解得：v_m=2.75m/s

故金属框下滑的最大速度为：v_m=2.75m/s．

（2）根据牛顿第二定律有：

mgsinα-μmgcosα-2BIL₂=ma

解得：I=0.6A

P=I²R=0.18W

故当金属框下滑的加速度为a=2m/s²时，金属框的焦耳热功率为：P=0.18W．

（3）下落过程，根据功能关系有：

W_G+W_f+W_安=

mv_t²-

mv₀²

mgssinα-μmgscosα-Q=

mv_m^{2
解得：Q=0.47J
故从开始下滑到速度达到最大的过程中金属框中产生的焦耳热量为：Q=0.47J．}