问题
问答题
一个带正电的微粒,从A点射入水平方向的匀强电场中,微粒沿直线由A向B运动,如图所示,AB与电场线夹角为θ.已知带电微粒的质量为m,电荷量为q,A、B相距L(重力加速度为g).
(1)试说明微粒在电场中运动的性质,要求说明理由.
(2)求电场强度的大小和方向?

答案
对微粒进行建立坐标系进行受力分析:
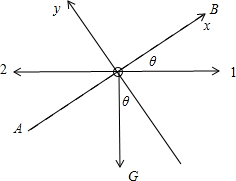
建立AB方向的x轴和垂直AB方向的y轴,因为微粒沿虚线AB运动,故在垂直AB的y轴方向的合力应该为0,因为微粒在电场中受重力和电场力作用,重力方向竖直向下,电场力可以沿1和2的方向,因为垂直y轴的方向合力为0,故微粒受电场力只能沿2方向.
x轴方向:F合=0-F电cosθ-Gsinθ=max ①
y轴方向:F合y=F电sinθ-Gcosθ=0 ②
(1)根据受力分析知,微粒所受合力沿x轴的负方向,因为物体沿AB运动也就是x轴的正方向,故微粒做匀减速直线运动;
(2)由②可知F电=
=mgcosθ sinθ mg tanθ
又因为F电=qE
所以E=
=F电 q mg qtanθ
又因为微粒带正电,受电场力沿图中2方向,故电场强度的方向和正电荷受力方向相同,即电场强度水平向左.
答:(1)微粒做匀减速直线运动,原因微粒在直线上运动且合力方向与运动方向相反;
(2)电场强度E=
方向水平向左.mg qtanθ
