问题
问答题
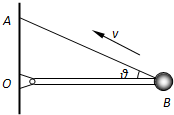
如图所示,某三角支架ABO中,轻杆BO可绕通过O点的光滑轴转动,AO⊥BO,AB间用细绳连接,θ=370.在B点连接质量为m=2kg的小球,杆AO在外力作用下保持竖直方向,且使整个装置沿BA方向做直线运动.已知重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8.
(1)当整个装置做匀速直线运动时,细绳AB和杆OB对小球作用力分别为多大?
(2)当整个装置以加速度a=g做匀减速运动时,轻绳AB和杆OB对小球作用力分别为多大?
答案
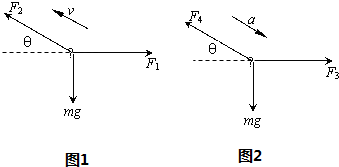
(1)当整个装置做匀速直线运动时,小球受力如图1所示,由平衡条件得:
F2sinθ=mg,
F2cosθ=F1.
解得:F1=
mg,F2=4 3
mg5 3
(2)沿加速度方向和加速度垂直的方向进行正交分解得:
F3sinθ=mgcosθ
F3cosθ+mgsinθ-F4=ma
解得:F3=
mg,F4=4 3
mg2 3
答:(1)当整个装置做匀速直线运动时,细绳AB和杆OB对小球作用力分别为
mg和5 3
mg.4 3
(2)当整个装置以加速度a=g做匀减速运动时,轻绳AB和杆OB对小球作用力分别为
mg和2 3
mg.4 3
