问题
问答题
如图所示,用完全相同的、劲度系数均为k的轻弹簧A、B、C将两个质量均为m的小球连接并悬挂起来,两小球均处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,已知重力加速度为g,试求出轻弹簧A、B、C各自的伸长量.(所有弹簧形变均在弹性范围内)
答案
将两小球看作一个整体,对整体受力分析,
可知整体受到重力2mg,弹簧A和C的拉力FA和FC的作用,受力如下图所示,
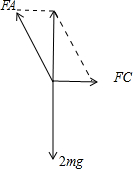
根据共点力的平衡条件有:
FA=
,FC=2mgtan30°2mg cos30°
根据胡克定律:FA=KXA,FC=KXC
联立以上各式得:弹簧AC的伸长量分别为:XA=
,XC=4
mg3 3k 2
mg3 3k
对BC间的小球进行受力分析,其受力如图乙所示,
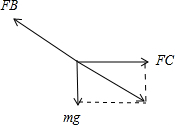
根据平衡条件由:FB=
=(mg)2+FC2
mg21 3
根据胡克定律有:FB=kxB,解得B的伸长量为:xB=
mg21 3k
答:轻弹簧A、B、C各自的伸长量分别为:XA=
,xB=4
mg3 3k
,XC=
mg21 3k
.2
mg3 3k
