问题
问答题
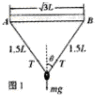
质量为M、长为
L的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳,绳上套着一质量为m的小铁环.已知重力加速度为g,不计空气影响.3
(1)现让杆和环均静止悬挂在空中,如图甲,求绳中拉力的大小:
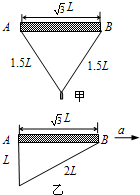
(2)若杆与环保持相对静止,在空中沿AB方向水平向右做匀加速直线运动,此时环恰好悬于A端的正下方,如图乙所示.
①求此状态下杆的加速度大小a;
②为保持这种状态需在杆上施加一个多大的外力,方向如何?
答案
(1)以环为研究对象,环处于静止状态,合力为零,分析受力右图所示,设两绳的夹角为2θ.
则sinθ=
=
L3 2 1.5L
,得cosθ=3 3
=1-sin2θ 6 3
设绳子的拉力大小为T,由平衡条件得
2Tcosθ=mg
解得,T=
mg6 4
(2)①对环:设绳子的拉力大小为T′,则根据牛顿第二定律得:
 竖直方向:T′+T′cos60°=mg
竖直方向:T′+T′cos60°=mg
水平方向:T′sin60°=ma,
解得a=
g3 3
②设外力大小为F,方向与水平方向成α角斜向右上方.
对整体:由牛顿第二定律得:
水平方向:Fcosα=(M+m)a
竖直方向:Fsinα=(M+m)g
解得,F=
(m+M)g,α=60°即外力方向与水平方向夹角为60°斜向右上方.2 3 3
答:(1)现让杆和环均静止悬挂在空中,绳中拉力的大小是
mg;6 4
(2)①此状态下杆的加速度大小a为
g;3 3
②为保持这种状态需在杆上施加一个的外力为
(m+M)g,方向与水平方向夹角为60°斜向右上方.2 3 3