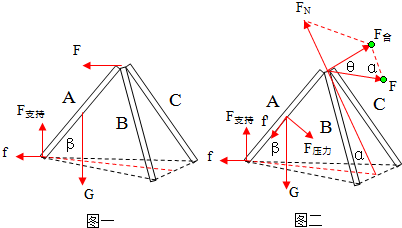
三根重均为G、长均为a的相同均匀木杆(其直径d≪a)如图对称地靠在一起,三木杆底端间均相距a,求:
(1)A杆顶端所受作用力的大小和方向,
(2)若有一重为G的人坐在A杆中点处,则A杆顶端所受作用力的大小和方向又如何?
三木杆组成一个正四面体,已知正四面体边长a,高三木杆h=a,
设杆与底面的夹角β,则cosβ=,sinβ=,
设BC的中垂线与底面的夹角是α,则sinα=,cosα=.
(1)以A杆为研究对象,A杆受力如图一所示.
A杆与地面的接触点为支点,杆所受重力G的力臂L重=cosβ=a,
杆顶端所受力F的力臂,LF=asinβ=a,由杠杆平衡条件,
得:GL重=FLF,即:G×a=F×a,F=G,方向水平向左.
(2)以A杆为研究对象,受力如图所示.由于人处于静止状态,
所以人对杆的压力F压力摩擦力f'大小等于人的重力G,方向竖直向下,
人对杆的作用力力臂L人=cosβ=a,
BC杆所组成面对杆的作用力FN,力臂等于四面体的高h,
LFN=h=a,由杠杆的平衡条件得:GL人+GL重=FLF+FNLFN,
即G×a+G×a=F×a+FN×a,解得:FN=G,
A杆顶端所受作用力的大小:
F合===G,
方向斜向右上方,如图所示.
答:(1)A杆顶端所受作用力的大小为F=G,方向水平向左.
(2)A杆顶端所受作用力的大小为G,方向斜向右上方,如图所示.