问题
问答题
一个重为20N的光滑小球A，静止在光滑斜面与竖直挡板之间，斜面的倾角为37度，求：
（1）小球对斜面的压力和对竖直挡板的压力；
（2）现将挡板P缓慢地由竖直位置逆时针转到水平位置，求此过程中球对挡板压力的最小值．（sin37°=
，cos37°=3 5
）4 5
答案
（1）对球受力分析如图所示：
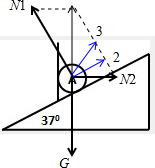
由于光滑圆球受共点力处于静止状态，所以光滑圆球的合力为0．
由共点力平衡的条件得出：
N1=
=G cos37°
=25N20 0.8
N2=Gtan37°=20×
=15N3 4
根据牛顿第三定律得：小球对斜面的压力为25N，对竖直挡板的压力为15N；
（2）将挡板P缓慢地由竖直位置逆时针转到水平位置，则挡板对球的弹力方向和大小如图中由初始位置到2到3过程变化，
由图可以看出当挡板与斜面垂直时所受挡板支持力最小：
Nmin=Gsin37°=10×0.6=12N
则球挡板压力的最小值为12N．
答：（1）小球对斜面的压力为25N，对竖直挡板的压力为15N；
（2）现将挡板P缓慢地由竖直位置逆时针转到水平位置，此过程中球对挡板压力的最小值为12N．
缺失，余留牙无异常，咬合关系良好，要求做
非贵金属烤瓷桥修复，比色A3