问题
问答题
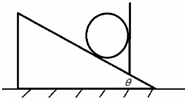
如图所示，水平桌面上有一斜面，斜面上固定了一竖直挡板，在挡板与斜面间如图放置一圆柱体，圆柱与斜面、挡板之间均不存在摩擦．已知斜面倾角θ=37°，斜面质量M=2kg，圆柱体质量m=1kg，桌面与斜面体之间的滑动摩擦因数μ=0.1．
（cos37°=0.8，重力加速度g=10m/s2）问：
（1）当斜面处于静止状态时，求圆柱体对斜面压力的大小和方向．
（2）现对斜面体施加一个水平向右的推力F使它们一起向右匀加速运动，为保证圆柱体不离开竖直挡板，求力F的最大值．
答案
（1）对圆柱体受力分析，如图所示．
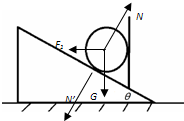
根据平衡条件得：
Ncosθ=G
Nsinθ=F1
则得：斜面对圆柱体的支持力 N=
=G cosθ
N=12.5N10 cos37°
根据牛顿第三定律得：圆柱体对斜面压力的大小为 N′=N=12.5N，方向垂直于斜面向下．
（2）当F增大时，整体水平向右加速，挡板弹力逐渐减小，当弹力减小到0时，达到临界状态，外力F达到最大值．
对圆柱体分析，根据牛顿第二定律得：
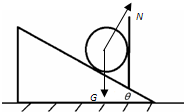Ncosθ=G
Nsinθ=ma
得a=7.5m/s2．
对整体分析
F-μ（Mg+mg）=（M+m）a
得F=（μg+a）（M+m）=（0.1×10+7.5）×（2+1）N=25.5N
答：
（1）当斜面处于静止状态时，圆柱体对斜面压力的大小为12.5N，方向垂直于斜面向下．
（2）现对斜面体施加一个水平向右的推力F使它们一起向右匀加速运动，为保证圆柱体不离开竖直挡板，力F的最大值是25.5N．