问题
问答题
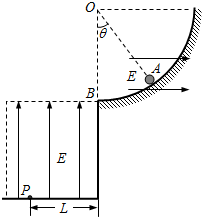
如图,绝缘的光滑圆弧曲面固定在竖直平面内,B为曲面最低点.曲面上的A点与曲面圆心O的连线与竖直方向成夹角θ=37°.曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上.开始时有一质量为m的带电小球处于A点恰好保持静止.此后将曲面内的电场撤去,小球沿曲面下滑至B点时以大小为v0的速度水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L.已知tan37°=0.75,重力加速度为g,求:
(1)小球的带电性及电荷量q.
(2)小球运动到P点瞬间的速度vP的大小.
答案
(1)带电小球静止在A点恰好静止,合力为零,根据平衡条件得知小球带正电.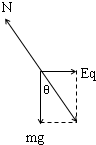
且有 qE=mgtanθ
解得 q=3mg 4E
(2)小球从B点水平抛出后做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速运动,则
水平方向:L=v0t
竖直方向:mg-qE=ma
vy=at
小球运动到P点瞬间的速度vP的大小为 v=
+v 20 v 2y
联立解得,v=
+(v 20
)2gL 4v0
答:
(1)小球带正电,电荷量q为
.3mg 4E
(2)小球运动到P点瞬间的速度vP的大小为
.
+(v 20
)2gL 4v0
