问题
填空题
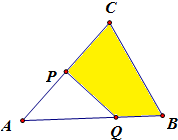
已知△ABC的面积为1,在△ABC所在的平面内有两点P、Q,满足
|
答案
∵点P满足
+PA
=PC
,0
∴
=-PA
,可得点P是线段AC的中点PC
又∵
+QA
+QB
=QC BC
∴
=QA
+BC
+CQ
=2BQ BQ
可得Q是线段AB的靠近B点的三等分点
因此,△APQ的面积为
S△APQ=
|1 2
|•|AP
|sinA=AQ
•1 2
|1 2
|•AC
|2 3
|=AB
S△ABC1 3
∵△ABC的面积为1,∴S△APQ=1 3
由此可得四边形BCPQ的面积为S=S△ABC-S△APQ=1-
=1 3 2 3
故答案为:2 3