特种兵过山谷的一种方法可化简为如图所示的模型:将一根长为2d、不可伸长的细绳的两端固定在相距为d的A、B两等高处,悬绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面.开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP竖直,则此时甲对滑轮的水平拉力为______;若甲将滑轮由静止释放,则乙在滑动中速度的最大值为______.(不计滑轮与绳的质量,不计滑辁的大小及摩擦)
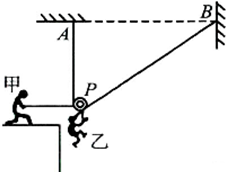
(1)对滑轮受力分析并正交分解如图:
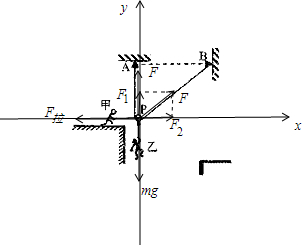
同一根绳上的拉力相等,故AP,BP绳上的拉力均为F
设AP的长度为:x,则BP长度为:2d-x
在直角三角形ABP中:
2=. BP
2+. AB
2. AP
即:(2d-x)2=d2+x2
解得:x=
d,即:AP长度为:3 4
d,BP长度为:3 4 5d 4
即:∠APB=53°
所以:F1=Fcos53°=0.6F
F2=Fsin53°=0.8F
由滑轮平衡得:
y方向:mg=F+F1=F+0.6F
解得:F=mg 1.6
x方向:F2=F拉,即:F拉=0.8×
=mg 1.6 mg 2
(2)甲将滑轮由静止释放后,战士乙只有重力对其做功,所以下落到最低点是速度最大,下落到最低点时,绳子如图
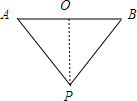
此时三条边均为d,三角形为正三角形,即:每个角为60°
所以此时P距离A点的竖直高度OP为:dsin60°=
d3 2
从静止到此状态战士乙共下落的高度h为:h=
d-3 2
d3 4
设此时的速度为v,在下落过程中只有重力做功,做的功为:mgh
由动能定理得:
mgh=
mv21 2
代入数据得:v=
=2gh
d)=2g(
d-3 2 3 4 (
-3
)gd3 2
故答案为:
;mg 2 (
-3
)gd3 2
