问题
填空题
已知向量a＝(1，n)，b＝(－1，n)，若2a－b与a＋2b垂直，则|a|＝________.
答案
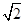
∵2a－b与a＋2b垂直，∴(2a－b)·(a＋2b)＝0，(3，n)·(－1,3n)＝0，∴－3＋3n2＝0，n2＝1，∴|a|＝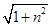
＝.
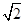搜题请搜索小程序“爱下问搜题”
已知向量a＝(1，n)，b＝(－1，n)，若2a－b与a＋2b垂直，则|a|＝________.
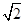
∵2a－b与a＋2b垂直，∴(2a－b)·(a＋2b)＝0，(3，n)·(－1,3n)＝0，∴－3＋3n2＝0，n2＝1，∴|a|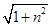＝＝.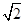