问题
选择题
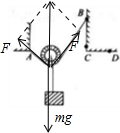
如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子中张力为T1,将绳子一端由B点移至C点,待整个系统重新达到平衡时,两段绳子间的夹角为θ2,绳子中张力为T2;再将绳子一端由C点移至D点,待整个系统再次达到平衡时,两段绳子间的夹角为θ3,绳子中张力为T3,不计摩擦,则( )
A.θ1=θ2=θ3
B.θ1<θ2<θ3
C.T1>T2>T3
D.T1=T2<T3
答案
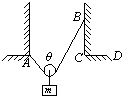
设绳子结点为O,对其受力分析,如图
当绳子右端从B移动到C点时,根据几何关系,有
AOsin
+OBsinθ1 2
=ACθ2 2
同理:AO′sin
+O′Bsinθ2 2
=ACθ2 2
绳子长度不变,有
AO+OB=AO′+O′B
故θ1=θ2
绳子的结点受重力和两个绳子的拉力,由于绳子夹角不变,根据三力平衡可知,绳子拉力不变,即T1=T2;
绳子右端从B移动到D点时,绳子间夹角显然变大,绳子的结点受重力和两个绳子的拉力,再次根据共点力
平衡条件可得T1<T3
故D正确,A、B、C错误.
故选D.