由

PA

+

PB

+

PC

=3

PG

⇔（

GA

-

GP

）+（

GB

-

GP

）+（

GC

-

GP

）-3

GP

=

0

⇔

GA

+

GB

+

GC

=

0

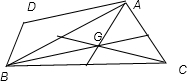
由题意画出简图为：

由于

GA

+

GB

+

GC

=

0

⇔

GA

+

GB

=

CG

，

在图形中，利用平行四边行法则及两向量的加法原理可知：GB为两相邻边的平行四边形的对角线GD，

由于四边形GADB为平行四边形，所以GD平分AB，所以点G在三角形ABC的边AB的中线上，

同理点G应该在BC边的中线上，利用重心的定义可知G是△ABC重心（即三条边上中线的交点）．

故选C．