问题
问答题
设函数f(x)在[0,+∞)上可导,且f(1)=3,若f(x)的反函数g(x)满足
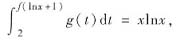
求f(x).
答案
参考答案:这是含变上限定积分的方程,两端对x求导得
[*]
因为f(x)与g(x)互为反函数,所以gf(u)]=u,从而上式变为
[*]
令1+lnx=t[*]x=et-1,且f’(t)=et-1,积分得f(t)=et-1+C.
由f(1)=3可得C=2,故f(x)=ex-1+2.
