问题
问答题
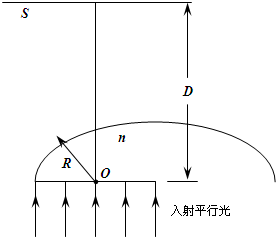
如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区.已知玻璃半球的半径为R,屏幕S至球心的距离为D(D>4R),不考虑光的干涉和衍射,试问:
(1)在屏幕S上形成的圆形亮区的最外侧是什么颜色?
(2)若玻璃半球对(1)中最外侧色光的折射率为n,请你求出圆形亮区的最大半径.
答案

(1)紫色.当平行光从玻璃中射向空气时,由于紫光的折射率的最大,则临界角最小,所以首先发生全反射,因此出射光线与屏幕的交点最远.故圆形亮区的最外侧紫光.
(2)如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到亮区中心G的距离r就是所求最大半径.设紫光临界角为C,
由全反射的知识得:sinC=
,1 n
又:AB=RsinC=
,R n
OB=RcosC=R
,BF=AB•tanC=n2-1 n
,GF=D-(OB+BF)=D-R n n2-1
,nR n2-1
=GE AB GF FB
所以有r=GE=
•AB=D•GF FB
-nR.n2-1
答:(1)在屏幕S上形成的圆形亮区的最外侧是紫光;
(2)若玻璃半球对(1)中最外侧色光的折射率为n,圆形亮区的最大半径为D•
-nR.n2-1
