问题
选择题
已知非零向量a，b，c满足a＋b＋c＝0，向量a与b的夹角为60°，且|a|＝|b|＝1，则向量a与c的夹角为( )．
A．30°
B．60°
C．120°
D．150°
答案
答案：D
因为a＋b＋c＝0，所以c＝－(a＋b)．所以|c|2＝(a＋b)2＝a2＋b2＋2a·b＝2＋2cos 60°＝3.所以|c|＝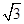
.
又c·a＝－(a＋b)·a＝－a2－a·b＝－1－cos 60°＝－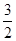
，设向量c与a的夹角为θ，则cos θ＝
＝
＝－
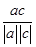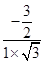.又0°≤θ≤180°，所以θ＝150°.
