问题
问答题
设函数
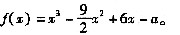
(1)对于任意实数x,f(x)≥m恒成立,求m的最大值;
(2)若方程f(x)=0有且仅有一个实根,求a的取值范围。
答案
参考答案:(1)f’(x)=3x2-9x+6=3(x-1)(x-2),
∵∈(-∞,+∞),f’(x)≥m,
即3x2-9x+(6-m)≥0恒成立,
∴△=81-12(6-m)≤0,
[*]
(2)∵当x<1时f’(x)>0;
当1<x<2时f’(x)<0;
当x>2时f’(x)>0,
∴当X=1时f(x)取极大值[*]
当x=2时f(x)取极小值f(2)=2-a,
故当f(2)>0或.f(1)<0时,方程f(x)=0仅有一个实根,
[*]
