设OD=a，OE=b，由余弦定理，得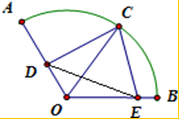CD²=CO²+DO²-2CO•DOcos60°=a²-a+1．

同理可得CE²=b²-b+1，DE²=a²+ab+b²

从而得到CD²+CE²+DE²=2（a²+b²）-（a+b）+ab+2=

26

9

∴2（a²+b²）-（a+b）+ab-

8

9

=0，

配方得2（a+b）²-（a+b）-3ab-

8

9

=0，即3ab=2（a+b）²-（a+b）-

8

9

…（*）

又∵ab≤[

1

2

（a+b）]²=

1

4

（a+b）²，

∴3ab≤

3

4

（a+b）²，代入（*）式，得2（a+b）²-（a+b）-

8

9

≤

3

4

（a+b）²，

设a+b=m，代入上式有2m²-m-

8

9

≤

3

4

m²，

即

5

4

m²-m-

8

9

≤0，得到-

8

15

≤m≤

4

3

，

∴m最大值为

4

3

，即OD+OE的最大值是

4

3

．