问题
计算题
如图所示，一根弹性细绳劲度系数为k （拉力和伸长量满足胡克定律），将其一端固定，另一端穿过一光滑小孔O系住一质量为m的滑块，滑块放在水平地面上。当细绳竖直时，小孔O到悬点的距离恰为弹性细绳原长，小孔O到水平地面的距离为h（h＜）,滑块与水平地面间的动摩擦因数为μ，试求当滑块静止时，距O 
点的最远距离为多少？（假设最大静摩擦力等于滑动摩擦力）
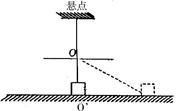
答案
解：如图设m距O 
点的最远距离为 r ,此时弹性绳与水平面的夹角为α，伸长量为L,其恰好静止时有
K·Lcosα=f
①
K·Lsinα＋F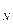
="mg " ②
f= 
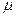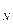·F ③
r= Lcosα ④
h=" Lsinα " ⑤
联立得r=
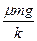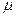－·h
所以m可以静止在水平面上以O
为圆心r为半径的园形区域内的任何位置。
