问题
计算题
如图所示,两根相同的橡皮绳OA、OB,开始夹角为0º,在O点处打结吊一重G=40 N的物体后,结点O刚好位于圆心。
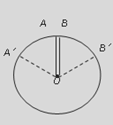
小题1:将A、B分别沿圆周向两边移至A′、B′,使∠AOA′=∠BOB′=60°。欲使结点仍在圆心处,则此时结点处应挂多重的物体?
小题2:若将橡皮绳换成无明显弹性的轻绳,结点仍在圆心O,在结点处仍挂重G=40 N的重物,并保持左侧轻绳在OA'不动,缓慢将右侧轻绳从OB'沿圆周移动,当右侧轻绳移动到什么位置时右侧轻绳中的拉力最小?最小值是多少?
答案
小题1:G=20N
小题2:Fmin=20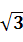 N
N
:(1)设OA、OB并排吊起重物时,橡皮条产生的弹力均为F,则它们的合力为2F,与G平衡,即2F=G,得 F=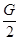 =20N.
=20N.
当∠AOA′=∠BOB′=60°时,∠A′OB′=120°时,橡皮条伸长不变,故F仍为20 N,它们互成120°角,合力的大小等于F,由平衡条件得知应挂G’="20" N的重物.
(2)以结点O为研究对象,分析受力可知:O点受三个力作用,重物对结点向下的拉力F=G,大小和方向都不变;左侧轻绳OA’的拉力FOA,其方向保持不变;右侧轻绳OB’的拉力拉力FOB.缓慢将右侧轻绳从OB’沿圆周移动时三力保持平衡.如图,由矢量三角形可知,当右侧轻绳移动到与左侧轻绳垂直时,右侧轻绳中的拉力最小,此时右侧轻绳与水平方向的夹角为θ=60°.由矢量直角三角形可知,拉力的最小值为:Fmin=Gsin60°=20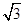 N.
N.
