问题
填空题
质量为 10 kg的环在F＝200 N的拉力作用下，沿粗糙直杆由静止开始运动，杆与水平地面的夹角θ＝37°，拉力F与杆的夹角也为θ。力F作用0.5s后撤去，环在杆上继续上滑了0.4s后，速度减为零。（已知sin37°＝0.6，cos37°＝0.8，g＝10 m/s2）求：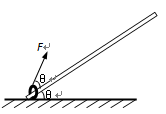
小题1:环与杆之间的动摩擦因数μ= ；
小题2:环沿杆向上运动的总距离s= m。
答案
小题1:0.5
小题2:1.8
分析：（1）环先沿杆做匀加速直线运动，后做匀减速直线运动．由题两个过程时间已知，根据运动学公式求出两段过程加速度关系．根据牛顿第二定律分别得到加速度的表达式，再联立求解μ．
（2）由位移公式分别求出两个过程的位移，位移之和等于环沿杆向上运动的总距离s．
解答：解：（1）设环做匀加速直线运动和匀减速直线运动的加速度大小分别为a1和a2，撤去力F瞬间物体的速度为v，
则由 v=a1t1和 0=v-a2t2
得a1t1=a2t2 代入得2a1=1.6a2①
根据牛顿第二定律得
Fcosθ-mgsinθ-μ（Fsinθ-mgcosθ）=ma1 ②
mgsinθ+μmgcosθ=ma2 ③
由①，②，③式联立解得 μ=0.5
（2）将μ=0.5代入②，③得
a1=8m/s2，a2=10m/s2
所以环沿杆向上运动的总距离s=
a1t12+a2t22=（×8×0.52+×10×0.42）m=1.8m．
答：（1）环与杆之间的动摩擦因数μ=0.5；
（2）环沿杆向上运动的总距离s=1.8m．
点评：本题应用牛顿第二定律和运动学规律结合处理动力学问题，第（1）问也可以用动量定理求解μ．