问题
问答题
一块足够长的木板，放在光滑水平面上.在木板上自左向右放有序号是1、2、3……n的木块，所有木块的质量均为m，与木板间的动摩擦因数都相同.开始时，木板静止不动，第1、2、3……n号木块的初速度分别为v0、2v0、3v0……nv0,v0方向都向右，如下图所示，木板的质量与所有木块的总质量相等，最终所有小木块都与木板以相同的速度匀速运动.求在整个过程中木板运动的最大速度.
答案
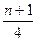v
所有木块在木板上相对木板滑动时对地的加速度相同，均为a=μg,各木块减速同时木板加速，木块先后顺序按1、2、3、4……n相对木板静止，只要有的木块还相对木板滑动，木板就加速.所以，当所有木块都相对木板静止时，木板运动的速度最大，设为vm.木块在木板上滑动过程中，所有木块与木板组成的系统动量守恒，由动量守恒定律选初末两状态便可求得vm.
所有木块与木板组成的系统动量守恒，当它们达共同速度时，木板达最大速度vm.
由动量守恒定律得
mv0+m·2v0+m·3v0+…+m·nv0=(n+n)mvm
所以vm=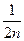
(1+2+3+…+n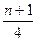)v0=v0.