用质量为M的铁锤沿水平方向将质量为m、长为l的铁钉敲入木板,铁锤每次以相同的速度v0击钉,随即与钉一起运动并使钉进入木板一定距离,在每次受击进入木板的过程中,钉所受的平均阻力为前一次受击进入木板过程所受平均阻力的k倍(k>1).
(1)若敲过三次后钉恰好全部进入木板,求第一次进入木板过程中钉所受到的平均阻力;
(2)若第一次敲击使钉进入木板深度为l1,问至少敲击多少次才能使钉全部进入木板?并就你的解答讨论要将钉全部敲入木板,l1必须满足的条件.
(1)
(2)n=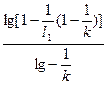 ,n为非整数,其取整加1;若恰为整数,则不加1.l1>(1-
,n为非整数,其取整加1;若恰为整数,则不加1.l1>(1-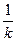 )l
)l
(1)铁锤每次击钉的短暂过程动量守恒,则有Mv0="(M+m)v " ①
其一起运动的初动能
Ek= (M+m)v2=
(M+m)v2= ·
· ②
②
设第一次进入木板过程中钉所受阻力为F,则第二次、第三次的阻力依次为kF、k2F,三次敲击后进入木板的深度依次为l1、l2和l3.根据动能定理,有Ek=Fl1=kFl2=k2Fl3 ③
l2=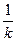 l1,l3=
l1,l3=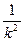 l1
l1
l1+l2+l3="l " ④
F=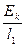 =
= ·
·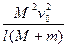 ·(1+
·(1+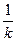 +
+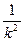 )=
)=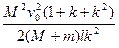 . ⑤
. ⑤
(2)设敲n次,钉全部进入木板,同理可得Ek=Fl1=kFl2=…=kn-1Fln
l1(1+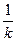 +
+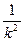 +…+
+…+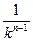 )="l " ⑥
)="l " ⑥
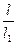 =1+
=1+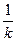 +
+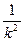 +…+
+…+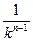 =
=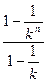 ⑦
⑦
n=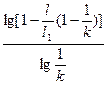 ⑧
⑧
若上式右边不是整数,n应为其取整加1;若恰为整数,则不加1.
⑦式右边随n增大而增大,但总是小于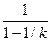 ,因而当l1太小时,无论多大的n也不能使⑦式成立,故要使钉能全部钉入木板,应有
,因而当l1太小时,无论多大的n也不能使⑦式成立,故要使钉能全部钉入木板,应有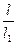 <
<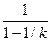 ,即l1>(1-
,即l1>(1-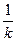 )l. ⑨
)l. ⑨
