问题
问答题
设x1＞0，
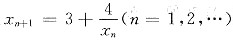，证明
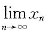存在，并求此极限值．
答案
参考答案：由x1＞0，[*]，可见xn+1＞3(n=1，2，…)．若[*]存在，记为a，则a≥3，对[*]两边取极限，得[*]，即a2-3a-4=0，得a=4，(a=-1舍弃)．
考虑[*]．
令n→∞，由夹逼定理得[*]，所以[*]存在且等于4．
搜题请搜索小程序“爱下问搜题”
设x1＞0，
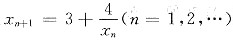，证明
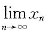存在，并求此极限值．
参考答案：由x1＞0，[*]，可见xn+1＞3(n=1，2，…)．若[*]存在，记为a，则a≥3，对[*]两边取极限，得[*]，即a2-3a-4=0，得a=4，(a=-1舍弃)．
考虑[*]．
令n→∞，由夹逼定理得[*]，所以[*]存在且等于4．