问题
问答题
设
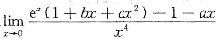存在，求常数a，b，c的值并求此极限值．
答案
参考答案：方法一：[*]．
若1+b-a≠0，则上式右边趋于∞．与题设矛盾，故1+b-a=0．再用洛必达法则，
[*]，
仿上讨论有1+2b+2c=0．继续用洛必达法则，
[*]，
仿上讨论有1+3b+6c=0．综合之，由以上3个等式解得[*]．以a，b，c之值代入，再由洛必达法则，可得原式极限[*]．
方法二：将ex在x0=0处按佩亚诺余项泰勒公式展开到o(x4)，有[*]，于是
[*]
可见上述极限存在的充要条件是
[*]．
解之a，b，c如方法一．以a，b，c之值代入，立即可得原式极限为[*]．
[注]：若式中有待定系数且用洛必达法则时，必须步步讨论，方法二比方法一方便、快捷．