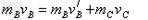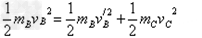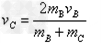问题
计算题
如图所示，粗糙斜面与光滑水平地面通过光滑小圆弧平滑连接，斜面倾角θ=37°，滑块A、C、D的质量均为m=1kg，滑块B的质量为mB=4kg，各滑块均可视为质点。A、B间夹着微量火药。K为处于原长的轻质弹簧，两端分别栓接滑块B和C。火药爆炸后，A与D相碰并粘在一起，沿斜面前进L=0.8 m时速度减为零，接着使其保持静止。已知滑块A、D与斜面间的动摩擦因数均为μ=0.5，运动过程中弹簧始终处于弹性限度内，取g=10 m/s2，sin37°=0.6，cos37°= 0.8。求：
(1)火药爆炸后A的最大速度vA；
(2)滑块B、C和弹簧K构成的系统在相互作用过程中，弹簧的最大弹性势能Ep；
(3)滑块C运动的最大速度vC。
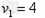
答案
解：（1）设A和D碰后的速度为v1，AD滑上斜面，由动能定理：
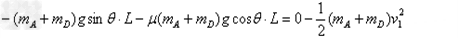
得：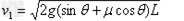
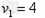m/s
火药爆炸后，A的速度最大为vA，由动量守恒定律有：
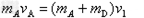
vA＝8m/s
（2）火药爆炸过程，对A和B系统，由动量守恒定律，设B获得的速度为vB
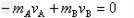
vB=2 m/s
当B与C共速为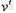
时，弹簧弹性势能最大
由B、C系统动量守恒，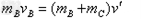
，
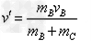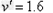m/s
弹簧的最大弹性势能为：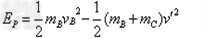
EP=1.6 J
（3）当弹簧为原长时，滑块C的速度最大为vC，则：
