(原创题)2009年12月26日起,武广高铁正式运行,由于电气化改造工程的技术标准较高,改造后列车运行速度加快、密度加大,因此对行车安全和人身安全提出了更高的要求.如图2-3-12所示为供电线路两电线杆之间电线覆冰后的情形,假设电线质量分布均匀,两电线杆正中间O处的张力为F,电线与电线杆结点A处的切线与竖直方向的夹角为θ,求:结点A处作用于电线的拉力大小FA为多少?两电杆间覆冰电线的质量为多大?
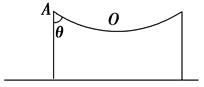
图2-3-12


法一:(合成法):如图甲所示,作出两电杆间左半部分覆冰电线的受力图.由“共面不平行的三个力平衡,则这三个力必为共点力”可知,这三个力为共点力.由三力平衡时,任意两力的合力应与第三个力平衡,故F与mg/2的合力应与FA平衡,设该合力与mg/2的夹角为θ,由平行四边形定则作出F与mg/2的合力,解直角三角形得:FA=F/sinθ,mg/2=Fcotθ,解出m=2Fcotθ/g.
法二:(效果分解法):如图乙所示,作出两电杆间左半部分覆冰电线的受力图.将重力沿F与FA的反方向分解,由力的平衡有,F=G1,FA=G2.解直角三角形得:G2=G1/sinθ,mg/2=G1cotθ,联立解出FA=F/sinθ,m=2Fcotθ/g.
法三:(正交分解法):如图丙所示,作出两电杆间左半部分覆冰电线的受力图.将拉力FA沿水平方向与竖直方向分解,由力的平衡有:F=FAsinθ,mg/2=FAcosθ,故解出FA=F/sinθ,m=2Fcotθ/g.

法四:(封闭三角形法):如图丁所示,左半部分覆冰电线受力平衡,受的三个力组成封闭的直角三角形,解直角三角形得:FA=F/sinθ,mg/2=Fcotθ,解出m=2Fcotθ/g.
