问题
问答题
如图，过椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．
试根据(1)中的结论猜测：椭圆
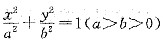的“左特征点”是一个怎样的点并证明你的结论．
答案
参考答案：
猜想：椭圆[*]的“左特征点”是椭圆的左准线与x轴的交点．
证明：设椭圆的左准线l与x轴相交于点M，过点A、B分别作l的垂线，垂足分别为点C、D．
据椭圆第二定义得，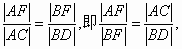
∵AC∥FM∥BD，∴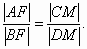
于是
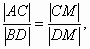即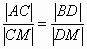
∴tan∠AMC=tan∠BMD，又∵∠AMC与∠BMD均为锐角，
∴∠AMC=∠BMD，∴∠AMF=∠BMF，∴MF为∠AMB的平分线．
故点M为椭圆的“左特征点”．
