问题
填空题
若向量
|
答案
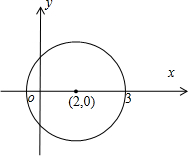
由题意设
=(2，0)，a
=(x，y)，b
∵|
-a
|=3，b
∴（x-2）2+y2=9，向量
满足，以（2，0）为圆心，半径为3的圆，b
|
|的几何意义是轨迹上的点到原点的距离，b
显然最大值为：5．
故答案为：5．
搜题请搜索小程序“爱下问搜题”
若向量
|
由题意设
=(2，0)，a
=(x，y)，b
∵|
-a
|=3，b
∴（x-2）2+y2=9，向量
满足，以（2，0）为圆心，半径为3的圆，b
|
|的几何意义是轨迹上的点到原点的距离，b
显然最大值为：5．
故答案为：5．