问题
问答题
一容器的内侧是由图中曲线绕y轴旋转一周而成的曲面,该曲线由
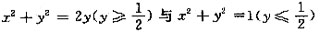 连接而成.
连接而成.
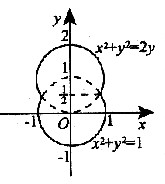
(Ⅰ)求容器的容积;
(Ⅱ)若将容器内盛满的水从容器顶部全部抽出,至少需要做多少功(长度单位:m,重力加速度为gm/s2,水的密度为103kg/m3)
答案
参考答案:(Ⅰ)方法一 由对称性,只须考察[*]部分,容器的边界曲线可表为[*],从而其容积
[*]
方法二 容器的边界曲线表可为
[*]
从而其容积
[*]
(Ⅱ)容器内侧曲线x=f(y)如题(Ⅰ)所示.在y轴上任取[y,y+dy],容器中对应薄片的水的重量为ρgπf2(y)dy(ρ为水的密度),它升高的距离d(y)=2-y.将此薄片抽出容器顶部所做的功为
dW=ρgπf2(y)(2-y)dy,
于是全部抽出容器内的水做的功为
[*]
其中
[*]
再代入上式得
[*]
