问题
填空题
设y=ex是微分方程xy’+p(x)y=x的一个解，则此微分方程满足
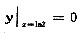的特解是______．
答案
参考答案：[*]
解析：
[分析]： 把y=ex代入xy’+p(x)y=x中，得xex+p(x)ex[*]x，因此p(x)=Xe-x-x．于是微分方程为xy’+(xe-x-x)y=z，即y’+(e-x-1)y=1，解此一阶线性微分方程，通解为
[*]
把[*]代入上式，得[*]，因此，所求特解为[*]