问题
问答题
设函数

(Ⅰ)当n为正整数,且nπ≤x<(n+1)π时,证明:2n≤S(x)<2(n+1);
(Ⅱ)求
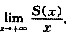
答案
参考答案:(Ⅰ)[证明] 由于|cosx|≥0及nπ≤x<(n+1)π,所以
[*]
又因|cosx|是以π为周期的函数,所以它在每个周期上的积分相等,因此
[*]
同理,[*]
从而 2n≤S(x)<2(n+1).
(Ⅱ)由(Ⅰ),当nπ≤x<(n+1)π时,有
[*]
又[*]以及当x→+∞时有n→∞.
由夹逼准则得
[*]