问题
计算题
(12分）如图，将质量m＝2kg的圆环套在与水平面成θ=37°角的足够长直杆上，直杆固定不动，环的直径略大于杆的截面直径，杆上依次有三点A.、B、C，sA.B=8m，sBC=0.6m，环与杆间动摩擦因数m＝0.5，对环施加一个与杆成37°斜向上的拉力F，使环从A.点由静止开始沿杆向上运动，已知t=4s时环到达B点。试求：（重力加速度g=l0m/s2，sin37°=0.6，cos37°=0.8）
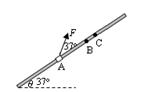
（1）F的大小；
（2）若到达B点时撤去力F，则环到达C点所用的时间。
答案
（1）20N（2）0.2s或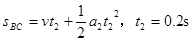
题目分析：（1）（8分）环做匀加速运动，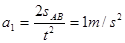
若Fsin370<Gcos370，杆对环的弹力在垂直杆向上，N＋Fsin37°＝mg cos37°，Fcos37°－mN－mg sin37°＝mA.，代入数据得，F＝20N
若Fsin370>Gcos370，杆对环的弹力在垂直杆向下，N＋mg cos37°＝Fsin37°
Fcos37°－mN－mg sin37°＝mA.，代入数据得，F=12N。不符合要求。（备注：得到20N正确，没有舍去12N扣1分）
（2）（4分）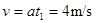
，μmgcosθ+mgsinθ=mA.2，A.2=μgcosθ+gsinθ=10m/s2，
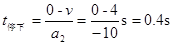，若物体向上经过C点，。
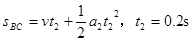若物体向下经过C点，mgsinθ-μmgcosθ=mA.3，A.3= gsinθ-μgcosθ=2m/s2，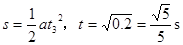
，
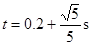，到C点的时间为0.2s或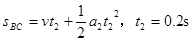
点评：在做力和运动题目时，加速度是关键，要么由加速度求力，要么由力求运动，