问题
问答题
设f(x)在[0，1]连续，在(0，1)内可导，且满足
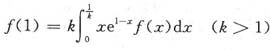
证明至少存在一点ξ∈(0，1)使得f’(ξ)=(1-ξ-1)f(ξ)．
答案
参考答案：题中即要证
[*]在(0，1)存在零点
[*]证明
[*]在(0，1)存在零点
即
[*]在(0，1)存在零点
[*]
(xe-x+cf(x))’在(0，1)存在零点
若能对F(x)=xe-x+cf(x)在[0，1](或[0，1]内某区间)用罗尔定理即可证明．为此改写假设条件
[*]
=ηe1-η(η)
按此想法给出如下证明．
令F(x)=xe1-xf(x)，按题设F(x)在[0，1]连续，在(0，1)可导，又
F(η)=ηe1-ηf(71)=f(1)=F(1)
于是F(x)在[η，1]上满足罗尔定理的条件，故存在ξ∈(η，1)[*](0，1)，使得F’(ξ)=0，即
ξe1-ξ[f’(ξ)-(1-ξ-1)f(ξ)]=0
即
f’(ξ)=(1-ξ-1)f(ξ)．