问题
计算题
如图所示,在足够长的光滑水平轨道上静止三个小木块A,B,C,质量分别为mA=1 kg,mB=1 kg,mC=2kg,其中B与C用一轻弹簧固定连接,开始整个装置处于静止状态。A和B之间有少许塑胶炸药,现引爆炸药,A,B将沿水平轨道运动,炸药爆炸产生的能量有E=9 J转化为A和B的动能,对于爆炸后A,B,C的运动。
(1)求A的速度的大小;
(2)求弹簧可能贮存的弹性势能的最大值;
(3)B有无向左运动的时刻?若有,求出B向左运动的最大速度。
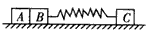
答案
解:(1)炸药爆炸的过程,A,B组成的系统动量守恒,设A,B获得的速度大小分别为vA,vB,有
mAvA=mBvB
又由能量的转化和守恒定律,有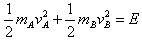
可解得vA=vB=3 m/s
(2)B与A分离后,B,C及弹簧组成的系统动量守恒、机械能守恒,设弹簧伸长(或压缩)最大时B,C的共同速度为vBC,此时贮存的弹性势能最大,设为Ep,有
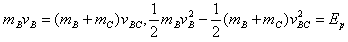
可解得Ep=3 J
(3)在以后的过程中,当弹簧由压缩恢复至原长时,B最有可能向左运动,设此时B,C的速度分别为vB,vC,取向右为正,由动量守恒定律有mBvB=mBvB'+mCvC'
由机械能守恒定律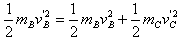
解得: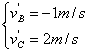 或
或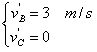 (舍去)
(舍去)
其中vB'= -1 m/s,为弹簧由压缩恢复至原长时的速度,即为B可能出现的向左的最大速度
