（1）由题意可得：a=

3

，c=

2

，b=1，∴r=

( 3 )2+12

=2．

∴椭圆C的方程为

x2

3

+y2=1，其“准圆”的方程为x²+y²=4；

（2）由“准圆”的方程为x²+y²=4，令y=0，解得x=±2，取点A（2，0）．

设点B（x₀，y₀），则D（x₀，-y₀）．

∴

AB

•

AD

=（x₀-2，y₀）•（x₀-2，-y₀）=(x0-2)2-y02，

∵点B在椭圆

x2

3

+y2=1上，∴

x02

3

+y02=1，∴y02=1-

x02

3

，

∴

AD

•

AB

=(x0-2)2-1+

x02

3

=

4

3

(x0-

3

2

)2，

∵-

3

＜x0＜

3

，∴0≤

4

3

(x0-

3

2

)2＜7+4

3

，

∴0≤

AD

•

AB

＜7+4

3

，即

AD

•

AB

的取值范围为[0，7+4

3

)

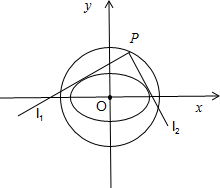
（3）①当过准圆上点P的直线l与椭圆相切且其中一条直线的斜率为0而另一条斜率不存在时，则点P为(±

3

，±1)，此时l₁⊥l₂；

②当过准圆上的点P的直线l的斜率存在不为0且与椭圆相切时，设点P（x₀，y₀），直线l的方程为m（y-y₀）=x-x₀．

联立

m(y-y0)=x-x0 x2 3 +y2=1

消去x得到关于y的一元二次方程：

(3+m2)y2+(2mx0-2m2y0)y+m2y02+x02-2mx0y0-3=0，

∴△=(2mx0-2m2y0)2-4(3+m2)(m2y02+x02-2mx0y0-3)=0，

化为(y02-1)m2-2mx0y0+x02-3=0，

∵y02-1≠0，m存在，∴m₁m₂=

x02-3

y02-1

．

∵点P在准圆上，∴x02+y02=4，∴x02-3=1-y02，

∴m₁m₂═-1．

即直线l₁，l₂的斜率kl1•kl2=-1，因此当过准圆上的点P的直线l的斜率存在不为0且与椭圆相切时，直线l₁⊥l₂．

综上可知：在椭圆C的“准圆”上任取一点P，过点P作直线l₁，l₂，使得l₁，l₂与椭圆C都只有一个交点，l₁⊥l₂．