问题
解答题
试用举反例的方法说明下列命题是假命题。
举例：如果ab＜0，那么a+b＜0
反例：设a=4，b=-3，ab=4×（-3）=-12＜0，而a+b=4+（-3）=1＞0
所以，这个命题是假命题。
（1）如果a+b＞0，那么ab＞0；
反例：
（2）如果a是无理数，b是无理数，那么a+b是无理数；
反例：
（3）两个三角形中，两边及其中一边的对角对应相等，则这两个三角形全等。
反例：（画出图形，并加以说明）
答案
解：（1）取a=2，b=-1，则a+b=1＞0，但ab=-2＜0，
所以此命题是假命题；
（2）取a=1+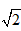
，b=1-
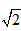，a、b均为无理数，
但a+b=2是有理数，所以此命题是假命题；
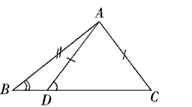
（3）如图所示，在△ABC与△ABD中，AB=AB，AD=AC，∠ABD=∠ABC，但△ABC与△ABD显然不全等，所以此命题是假命题。
