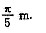问题
问答题
如下图所示，跷跷板AB的一端B碰到地面时，AB与地面的夹角为18°，且OA=OB=2m
（1）求此时另一端A离地面的距离（精确到0.1m）；
（2）跷动AB，使端点A碰到地面，画出点A运动的路线（写出作法，保留作图痕迹），并求出端点A运动路线的长（结果含π）．
（参考数据：sin18°≈0.31，cos18°≈0.95）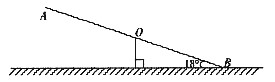
答案
参考答案：
(1)过点A作地面的垂线，垂足为C．
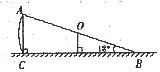
在Rt△ABC中，∠ABC=18°，
∴AC=AB·sin∠ABC
=4·sin18°
≈4×0.31
≈1.2．
答：另一端A离地面的距离约为1.2m．
(2)以点0为圆心，0A的长为半径画弧，交地面于点D，则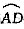
就是端点A运动的路线(C、D重合)．
端点A运动路线的长为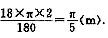
答：端点A运动路线的长为