阅读下列说明，回答问题1至问题3，将解答填入对应栏内。
【说明】
某餐厅供应各种标准的营养套餐。假设菜单上共有n项食物m1，m2，…，mn，每项食物mi的营养价值为vi，价格为pi其中i＝1，2，…，n，套餐中每项食物至多出现一次。客人常需要一个算法来求解总价格不超过M的营养价值最大的套餐。
| 【问题3】 问题1中伪代码的时间复杂度为 (6) (用O符号表示)。 |
参考答案：
解析：(6)O(nM)，或O(n×M)，或O(n*M)
试题四
[分析]：
本题实质上是一个0-1背包问题，该最优化问题的目标函数是
max
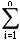ViXi(Xi＝0，1)
i＝1
约束函数是
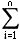PiXi≤M (xi＝0,1)
0-1背包问题可用动态规划策略求得最优解，求解的递归式为
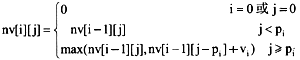
其中，nv[i][j]表示由前i项食物组合且价格不超过j的套餐的最大营养价值。问题最终要求的套餐的最大营养价值为nv[n][M]。根据上述递归式，可以很容易以自底向上的方式编写伪代码。[问题1]中伪代码的第1行到第12行计算数组nv的元素值，第1行到第4行计算i为0或者j为0时nv[i][j]的值，对应递归式的第一种情况；第7行和第8行计算当j＜pi时即不能选择mi时nv[i][j]的值，对应递归式的第二种情况：第9到第12行对应递归式的第三种情况，故根据递归式，空(1)的答案为nv[i-1][j]≥nv[i-1][j-p[i]] +v[i]。伪代码的第13行到第19行求解哪些食物放入到套餐中，食物项从后向前考虑，若nv[i][j]＝nv[i-1][j]，表示食物mi没有放入套餐中，即x[i]＝0，故空(2)的答案为nv[i][j]＝nv[i-1][j]。相反，若食物mi放入套餐中，则x[i]＝1，同时套餐还能选择不超过j-p[i]的价格的食物，故空(3)的答案为j＝j-p[i]。
问题2的实例要求总价格不超过100，根据上述递归式，计算出要选择的食物项为 m2、m3和m4，对应的总价值为605，总价格为100。
根据问题1的伪代码，第1行到第2行、第3行到第4行以及第14行到19行的时间复杂度为O(n)，第5行到第12行的时间复杂度为O(nM)。故算法总的时间复杂度为 O(nM)。