问题
计算题
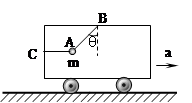
如图所示，AB、AC为不可伸长的轻绳，小球质量为m="0.4" kg．当小车静止时，AC水平，AB与竖直方向夹角为θ=37°，试求小车分别以下列加速度向右匀加速运动时，两绳上的张力FAC、FAB分别为多少．（取g="10" m／s2。sin370=0.6,cos370=0.8） (1)a1="5" m／s2。 (2)a2="10" m／s2。
答案
（1）FAB=5N FAC="1N" （2）5.7N
题目分析：设绳AC水平且拉力刚好为零时，临界加速度为a0
据牛顿第二定律
FABsin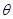
=ma0 ①
FABcos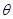="mg" ②
联立①、②两式并代入数据得 a0=7.5m/s2
（1）当a1=5m/s2< a0，此时AC绳伸直且有拉力。
据牛顿第二定律
FABsin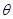－FAC= ma1 ③
FABcos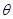="mg" ④
联立③、④两式并代入数据得
FAB=5N
FAC="1N"
（2）当a2=10m/s2>a0，此时AC绳不能伸直，F′AC=0。
AB绳与竖直方向夹角a>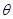
据牛顿第二定律
F′ABsina=ma2 ⑤
F′ABcosa=mg ⑥
联立⑤⑥式并代入数据得F′AB=5.7N（5.6N、4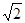
）