问题
问答题
某机械厂装配车间生产甲、乙两种产品,两种产品的全部产量每月至少要达到30台,规定甲、乙两种产品的产量比不能大于2,装配一台甲产品的劳动消耗为144人时,一台乙产品的劳动消耗72人时。该车间总的劳动资源为7 200人时,装配一台甲产品的成本为1 500元,一台乙产品的成本为900元,若要实现最低生产成本,甲、乙应各生产多少?(要求甲乙必须均生产)
答案
参考答案:解:设甲生产X台,乙生产Y台。
约束条件:X+Y≥30
X/Y≤2
144X+72Y≤7200
X,Y≥0
目标函数:成本=1500X+900Y
可行解域如下图阴影部分所示:
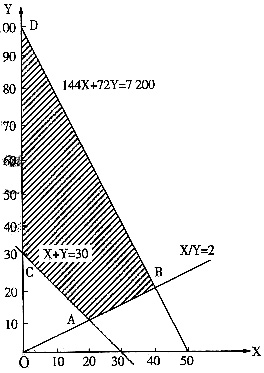
得A,B,C,D点,有
A点:X=20,Y=10,成本=1500×20+900×10=39000(元)
B点:X=40,Y=20,成本=1500×40+900×20=78000(元)
C点:X=0,Y=30,成本=1500×0+900×30=27000(元)
D点:X=0,Y=100,成本=1500×0+900×100=90000(元)
因为甲、乙必须生产,故当X=20,Y=10时成本最低,为39000元。
