问题
计算题
(8分)如图所示,一根长L=1.5 m的光滑绝缘细直杆MN,竖直固定在场强为E=1.0×105 N/C、与水平方向成θ=30°角的倾斜向上的匀强电场中。杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6 C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10一6 C,质量m=1.0×10一2 kg。现将小球B从杆的上端N静止释放,小球B开始运动。(静电力常量k=9.0×109 N·m2/C2,取g=l0 m/s2)
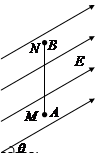
(1)小球B的速度最大时,距M端的高度h1为多大?
(2)小球B从N端运动到距M端的高度h2=0.6l m的P点时(图中未画出P点),速度为v=1.0 m/s,若取N点的电势为零,求P点的电势
答案
(1)0.9m (2)84000V
题目分析:(1)小球速度最大时,合力为零:
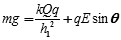
代入数据解得: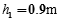
(2)对从N到P过程由动能定理得
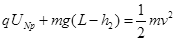
UNp=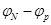
代入数据解得: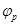 =84000V
=84000V
