问题
计算题
如图,竖直放置的大圆环圆心为O,半径为R,质量为m的小球A套在大圆环上,有一足够长的细轻绳拴在A上,另一端跨过固定在大圆环最高点C处的一个小滑轮后吊着一个小球B,不计滑轮半径和质量、不计绳子的质量,不计一切摩擦,绳子不可伸长.平衡时弦CA所对的圆心角θ=30°。
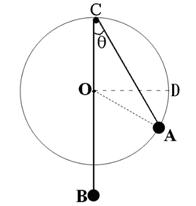
求:(1)小球B质量mB
(2)若mB=m,将小球A从圆心O的等高点D静止释放后小球A、B轨道稍微错开互不影响,求小球A的最大速度vAM。(可含根式)
答案
(1)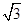 m (2)
m (2)
题目分析:(1)绳子拉力T=mB g=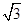 mg(3分)
mg(3分)
∴mB =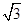 m(2分)
m(2分)
(2)A到达最低点时为最大速度vAM
此时vB=0(1分)动能定理
: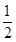 mvAM2=mgR-mg(2R-
mvAM2=mgR-mg(2R-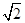 R) (2分)
R) (2分)
∴vAM= (2分)
(2分)
