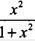问题
填空题
已知
|
答案
设
=(x,y),b
∵|
|=1,∴b
=1,即x2+y2=1.①x 2+y 2
∵
•a
=(b
,1 2
)•(x,y)=3 2
x+1 2
y=3 2
,3 2
∴x+
y=3
,即x=3
-3
y.②3
将②代入①得(
-3
y)2+y2=1,3
化简得4y2-6y+2=0,即2y2-3y+1=0.
解之得y1=
,y2=1.1 2
再代入②,可得x1=
,x2=0.3 2
∴
=(b
,3 2
)或1 2
=(1,0).b
故答案为::(
,3 2
)或(1,0)1 2

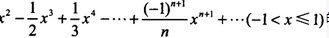 的和是()。
的和是()。