问题
计算题
（19分）如图所示平面直角坐标系xoy位于竖直平面内，在坐标系的整个空间存在竖直向上的匀强电场，在区域Ⅰ(0≤x≤L)还存在匀强磁场，磁场方向垂直于xoy平面向里。在x轴上方有一光滑弧形轨道PQ，PQ两点间竖直高度差为
。弧形轨道PQ末端水平，端口为Q (3L，
)；某时刻一质量为m、带电荷量为+q的小球b从y轴上的M点进入区域I，其速度方向沿x轴正方向；小球b在I区内做匀速圆周运动。b进入磁场的同时，另一个质量也为m、带电荷量为-q的小球a从P点由静止释放。两小球刚好在x=2L上的N点（没具体画出）反向等速率相碰。重力加速度为g。
求：(l)电场强度E；
(2)a球到达N点时的速度v；
(3)M点的坐标。
答案
（1）
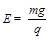（2）
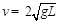与水平方向夹角为
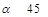（3）（0，
）
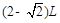题目分析：（1）有小球b在Ⅰ区做匀速圆周运动，有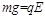
，解得：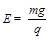
（2）设a小球到Q处的水平速度为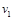
，则a小球从P到Q，由动能定理得：
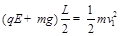解得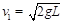
a小球从P到Q，做类平抛运动，加速度为a
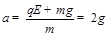
在x方向：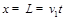
在y方向：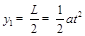
t时刻y方向的分速度为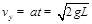
a小球到N时的速度的大小为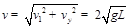
速度与水平方向夹角为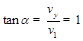
则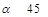
（3）由于a、b两小球刚好在x=2L上的N点（没具体画出）反向等速率相碰，则b在离开磁场A位置时速度也为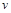
，且方向与x轴成45°，如图所示
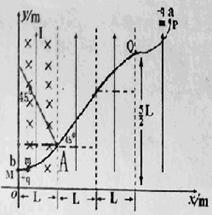
由几何关系得b在磁场中的轨迹半径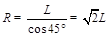
A到x的距离为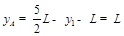
M到x的距离为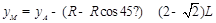
即M点的坐标为（0，）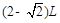
