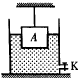
一带阀门的圆柱形容器,底面积是300cm2,装有13cm深的水.正方体A边长为12cm,重25N,用细绳悬挂放入水中,有1/6的体积露出水面,如图所示.试求:
(1)A受到的浮力,此时水对容器底部的压强.
(2)若细绳所能承受的最大拉力是14.92N,通过阀门K缓慢放水,当绳子刚要被拉断的瞬间,容器中液面下降的高度.(取g=10N/kg)
(1)容器中水的体积为:V水=SH=3.0×10-2m2×0.13m=3.9×10-3m3,正方体的体积为VA=L3=1.728×10-3m3.
①A受到的浮力为:F浮=
ρ水gVA=5 6
×1.0×103kg/m3×10N/kg×1.728×10-3m3=14.4N.5 6
设A放入水中后水深为H′,则有SH′=V水+
VA,则3.0×10-2m2×H′=3.9×10-3m3+5 6
×1.728×10-3m3.5 6
解得H′=0.178m.
此时水对容器底部的压强P=ρ水gH′=1.0×103kg/m3×10N/kg×0.178m=1.78×103Pa.
答:A受到的浮力为14.4N.此时水对容器底部的压强为1.78×103Pa.
(2)初始A浸入水中深度为h0=
L=5 6
×12cm=10cm.5 6
当绳子刚被拉断时有:Fm+F浮′=G,所以F浮′=25N-14.92N=10.08N.
设此时A浸入水中深度为h,则有F浮′=ρ水gL2h.
即10.08N=1.0×103kg/m3×10N/kg×0.12m×0.12m×h
解得h=0.07m=7cm,△h=h0-h=10cm-7cm=3cm.
答:容器中液面下降的高度为3cm.
